Question
Given two integer arrays nums1 and nums2, both sorted in non-decreasing order, and two integers m and n representing the number of elements in nums1 and nums2 respectively.
Merge nums1 and nums2 into a single array sorted in non-decreasing order and store the final sorted array inside the array nums1. To accommodate this, ensure that nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and ignore the last n elements, setting them to 0. nums2 has a length of n.
Example 1
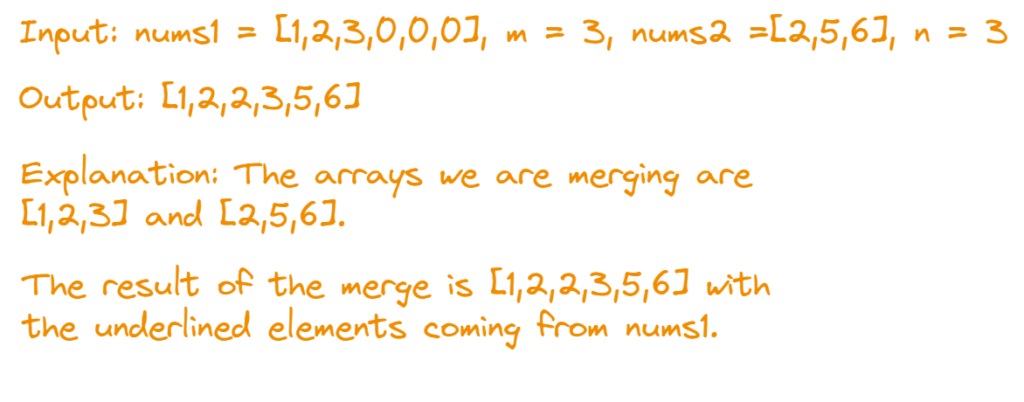
Constraints
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
Brute-force Solution
- We append all elements of
nums2to the end ofnums1starting from indexm. - We sort the entire
nums1array usingArrays.sort
Optimized Solution
Let’s do it step by step
- Initialization:
- We initialize three pointers:
index1: Starting from the last element ofnums1that needs to be merged (m - 1).index2: Starting from the last element ofnums2(n - 1).mergeIndex: Starting from the last index of the mergednums1(m + n - 1).
- We initialize three pointers:
- Merging:
- We iterate through both arrays starting from the ends (from the largest elements to the smallest).
- At each step, we compare the elements pointed by
index1innums1andindex2innums2. - We place the larger element at
mergeIndex, and then decrement the corresponding index (index1orindex2) to move to the next element. - We repeat this process until we have processed all elements from both arrays.
- Handling Remaining Elements:
- After the first loop, if there are any remaining elements in
nums2(i.e.,index2 >= 0), it means that all elements innums1have been merged, but there are still some elements innums2that need to be copied. - In this case, we copy the remaining elements directly into the beginning of
nums1, starting frommergeIndexand decrementing bothmergeIndexandindex2untilindex2becomes less than 0.
- After the first loop, if there are any remaining elements in
- Result:
- After this process, the merged
nums1array contains all elements from both arrays merged in non-decreasing order.
- After this process, the merged
Dry Run
1.We have two sorted arrays `nums1` and `nums2` :
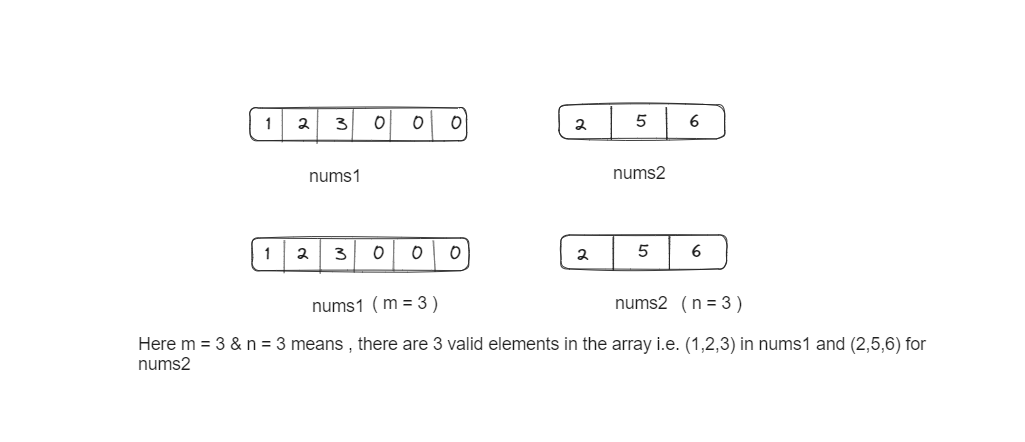
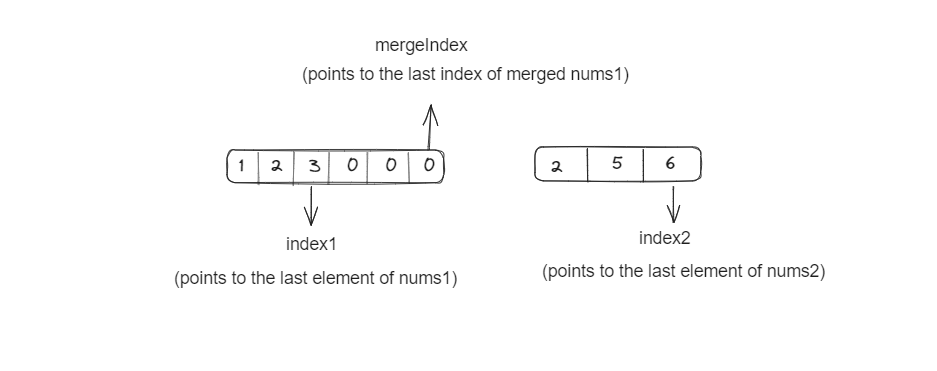
2. We will initialize three pointers: index1, index2, and mergeIndex:
index1 : m - 1 = 3-1 = 2
index2 : n-1 = 3-1 = 2
mergeIndex : m+n-1 = 3+3-1 = 5
3. We compare the elements at index1 and index2 and place the larger one at mergeIndex:
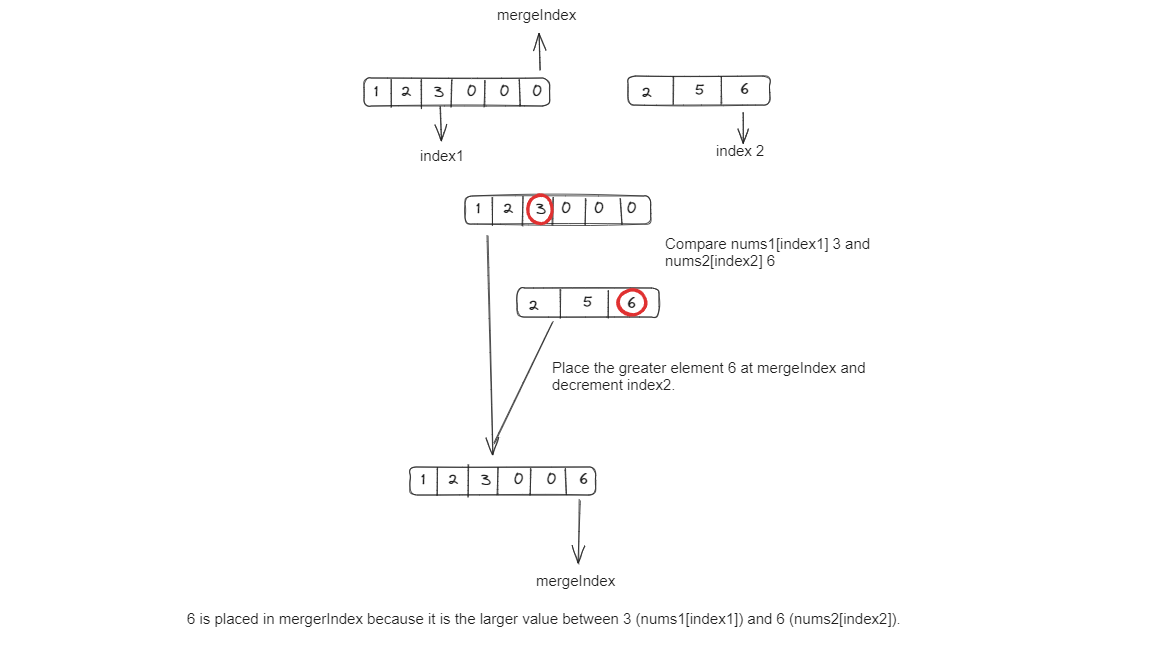
4. We continue this process until all elements are merged.
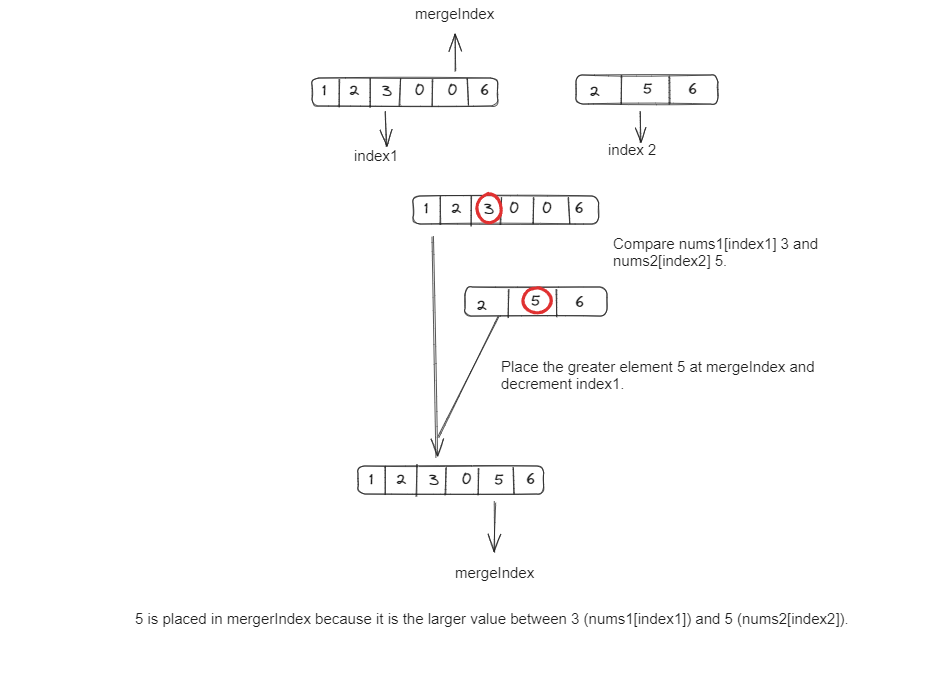
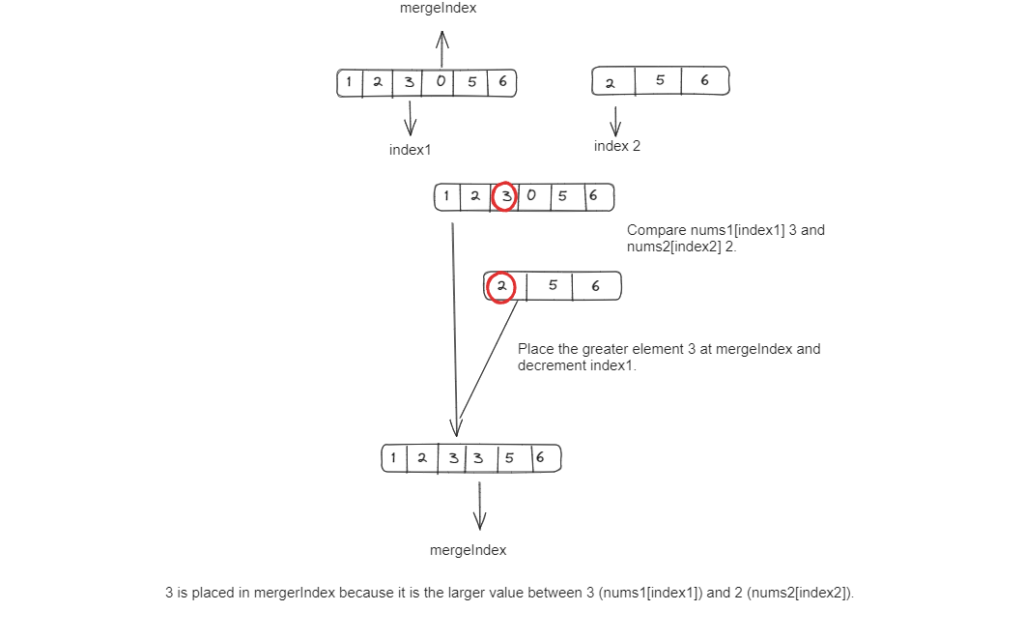
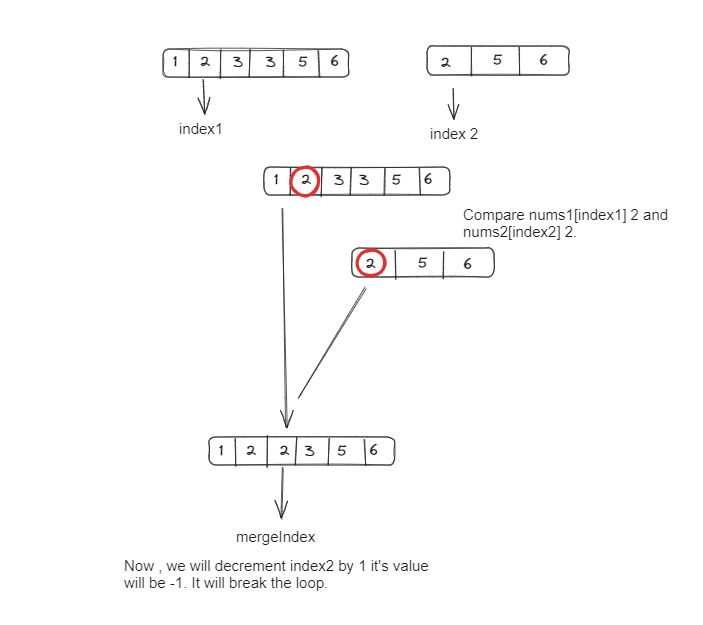
6. Finally, the merged nums1 array contains all elements in non-decreasing order.
Code
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int index1 = m - 1;
int index2 = n - 1;
int mergeIndex = m + n - 1;
while (index1 >= 0 && index2 >= 0) {
if (nums1[index1] > nums2[index2]) {
nums1[mergeIndex] = nums1[index1];
index1--;
} else {
nums1[mergeIndex] = nums2[index2];
index2--;
}
mergeIndex--;
}
while (index2 >= 0) {
nums1[mergeIndex] = nums2[index2];
index2--;
mergeIndex--;
}
}
}Complexity
- Time complexity: O(m + n)
- Space complexity: O(1)

